Zadanie nr 9930847
Uzasadnij, że jeżeli liczba całkowita jest nieparzysta, to jej kwadrat przy dzieleniu przez 8 daje resztę 1.
Rozwiązanie
Sposób I
Jeżeli 
jest liczbą nieparzystą, to jest postaci 
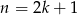. Wtedy
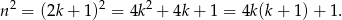
Zauważmy teraz, że liczba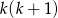 
jest zawsze parzysta (jako iloczyn dwóch kolejnych liczb całkowitych), więc liczba 
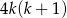jest liczbą podzielną przez 8. To oznacza, że liczba 
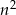rzeczywiście daje resztę 1 przy dzieleniu przez 8.
Sposób II
Zauważmy, że wystarczy wykazać, że liczba
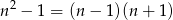
jest podzielna przez 8. Jeżeli 
jest liczbą nieparzystą, to liczby 
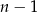i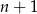 
są kolejnymi liczbami parzystymi, więc jedna z nich jest podzielnia przez 4. To oznacza, że powyższy iloczyn jest podzielny przez 
.
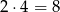