Zadanie nr 2030298
Dany ciąg arytmetyczny 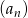 taki, że
taki, że 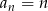 , dla
, dla 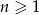 . Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez
. Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez 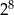 .
.
Rozwiązanie
Wyrazami ciągu 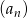 są kolejne liczby naturalne, więc iloczyn dziesięciu kolejnych wyrazów tego ciągu to po prostu iloczyn dziesięciu kolejnych liczb naturalnych.
są kolejne liczby naturalne, więc iloczyn dziesięciu kolejnych wyrazów tego ciągu to po prostu iloczyn dziesięciu kolejnych liczb naturalnych.
Zauważmy, że wśród dziesięciu kolejnych liczb naturalnych na pewno jest liczba podzielna przez 8, oprócz tej liczby jest jeszcze jedna liczba podzielna przez 4 (bo wśród dziesięciu kolejnych liczb są dwie podzielne przez 4). Poza tym są jeszcze 3 inne liczby parzyste (bo wśród dziesięciu kolejnych liczb jest 5 parzystych). Zatem iloczyn dziesięciu kolejnych wyrazów ciągu 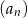 na pewno dzieli się przez
na pewno dzieli się przez