Zadanie nr 2252128
Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych nie dzieli się przez 4.
Rozwiązanie
Oznaczmy dwie kolejne liczby nieparzyste przez 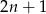 i
i 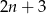 . Mamy wtedy
. Mamy wtedy
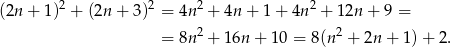
Ponieważ pierwszy składnik tej sumy dzieli się przez 4, a 2 nie dzieli się przez 4, całe wyrażenie nie może dzielić się przez 4.

