Zadanie nr 9165692
Uzasadnij, że suma kwadratów trzech kolejnych liczb parzystych nigdy nie jest liczbą podzielną przez 3.
Rozwiązanie
Oznaczmy trzy kolejne liczby parzyste przez 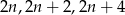 . Obliczamy sumę kwadratów tych liczb.
. Obliczamy sumę kwadratów tych liczb.
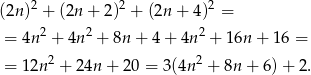
Widać teraz, że liczba ta nigdy nie dzieli się przez 3.

