Zadanie nr 9491505
Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
Rozwiązanie
Trzy kolejne liczby naturalne możemy oznaczyć przez 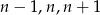 . Zatem ich suma sześcianów jest równa
. Zatem ich suma sześcianów jest równa
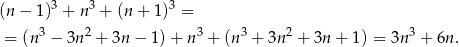
Sposób I
Ponieważ
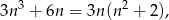
Wystarczy pokazać, że liczba 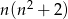 dzieli się przez 3.
dzieli się przez 3.
Jeżeli  dzieli się przez 3, to koniec.
dzieli się przez 3, to koniec.
Jeżeli  daje resztę 1 z dzielenia przez 3, czyli
daje resztę 1 z dzielenia przez 3, czyli 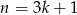 to
to
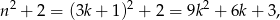
więc 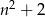 dzieli się przez 3.
dzieli się przez 3.
Jeżeli natomiast  daje resztę 2 z dzielenia przez 3, czyli
daje resztę 2 z dzielenia przez 3, czyli 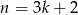 to
to
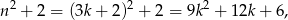
więc tak jak poprzednio, 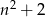 dzieli się przez 3.
dzieli się przez 3.
Sposób II
Ponieważ
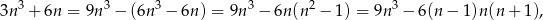
wystarczy pokazać, że 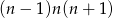 dzieli się przez 3. To jednak jest oczywiste, bo jest to iloczyn trzech kolejnych liczb całkowitych.
dzieli się przez 3. To jednak jest oczywiste, bo jest to iloczyn trzech kolejnych liczb całkowitych.

