Zadanie nr 2492023
Pokazać, że dla każdej liczby naturalnej  liczba
liczba 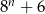 jest podzielna przez 7.
jest podzielna przez 7.
Rozwiązanie
Sposób I
Zauważmy, że
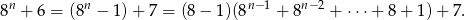
Widać teraz wyraźnie, że liczba ta dzieli się przez 7.
Sposób II
Zadanie łatwo można rozwiązać indukcyjnie. Sprawdzamy dla 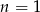 (lub
(lub 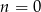 ) i zakładamy, że
) i zakładamy, że 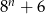 dzieli się przez 7. Mamy wtedy
dzieli się przez 7. Mamy wtedy
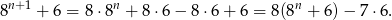
Wyrażenie w nawiasie dzieli się przez 7 z założenia indukcyjnego, reszta też, więc kończy to dowód indukcyjny.
Sposób III
Ponieważ 8 daje resztę 1 z dzielenia przez 7 (tzn. 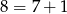 ), to taką samą resztę daje dowolna potęga 8 (reszta potęgi liczby to potęga reszty). Zatem całe wyrażenie daje resztę
), to taką samą resztę daje dowolna potęga 8 (reszta potęgi liczby to potęga reszty). Zatem całe wyrażenie daje resztę 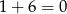 . Całe to rozumowanie wygodnie zapisuje się przy pomocy kongruencji
. Całe to rozumowanie wygodnie zapisuje się przy pomocy kongruencji
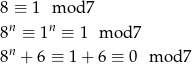
Korzystaliśmy z tego, że kongruencje można potęgować i dodawać stronami.

