Zadanie nr 3337696
Wykaż, że dla każdej liczby naturalnej 
liczba 
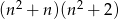jest podzielna przez 6.
Rozwiązanie
Zapiszmy dane wyrażenie w postaci
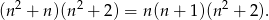
Zauważmy najpierw, że powyższa liczba na pewno jest parzysta: albo 
jest parzyste, albo parzysta jest liczba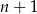 
.
Wystarczy zatem wykazać, że liczba ta dzieli się przez 3. Jeżeli 
lub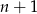 
dzieli się przez 3, to sprawa jest oczywista, więc załóżmy, że 
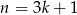. Mamy wtedy
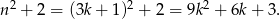
Widać teraz, że liczba ta dzieli się przez 3, więc rzeczywiście dana liczba dzieli się przez 6.
