Zadanie nr 4945083
Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 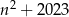 jest podzielna przez 8.
jest podzielna przez 8.
Rozwiązanie
Sposób I
Jeżeli  jest liczbą nieparzystą, to możemy ją zapisać w postaci
jest liczbą nieparzystą, to możemy ją zapisać w postaci 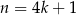 lub
lub 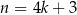 . W pierwszym przypadku
. W pierwszym przypadku
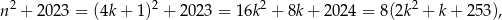
a w drugim
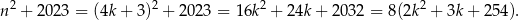
W obu przypadkach otrzymaliśmy więc liczbę podzielną przez 8.
Sposób II
Jeżeli  jest liczbą nieparzystą, to możemy ją zapisać w postaci
jest liczbą nieparzystą, to możemy ją zapisać w postaci 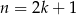 . Mamy wtedy
. Mamy wtedy
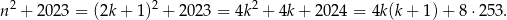
Teraz wystarczy zauważyć, że liczba 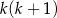 jest zawsze parzysta – bo jest to iloczyn dwóch kolejnych liczb całkowitych. To oznacza, że faktycznie liczba
jest zawsze parzysta – bo jest to iloczyn dwóch kolejnych liczb całkowitych. To oznacza, że faktycznie liczba 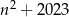 jest zawsze podzielna przez 8.
jest zawsze podzielna przez 8.

