Zadanie nr 7715374
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 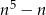 jest podzielna przez 30.
jest podzielna przez 30.
Rozwiązanie
Musimy pokazać, że liczba ta dzieli się przez 2,3 i 5.
Sposób I
Rozkładamy podane wyrażenie
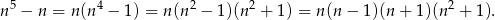
Ponieważ 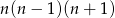 jest iloczynem trzech kolejnych liczb całkowitych, jedna z nich na pewno dzieli się przez 2 i jedna dzieli się przez 3. Pozostała do wykazania podzielność przez 5.
jest iloczynem trzech kolejnych liczb całkowitych, jedna z nich na pewno dzieli się przez 2 i jedna dzieli się przez 3. Pozostała do wykazania podzielność przez 5.
Jeżeli liczba  daje przy dzieleniu przez 5 resztę 0, 1 lub 4, to jedna z liczb w pierwszych trzech nawiasach dzieli się przez 5. Jeżeli natomiast
daje przy dzieleniu przez 5 resztę 0, 1 lub 4, to jedna z liczb w pierwszych trzech nawiasach dzieli się przez 5. Jeżeli natomiast 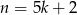 lub
lub 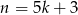 to
to
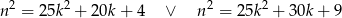
i liczba 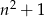 dzieli się przez 5.
dzieli się przez 5.
Sposób II
Robimy podobnie jak poprzednio, ale używamy odrobinę innego rozkładu.
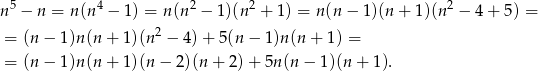
Pierwszy składnik jest iloczynem 5 kolejnych liczb całkowitych jest więc podzielny przez 2,3,5. Drugi w oczywisty sposób jest podzielny przez 5 i jako iloczyn 3 kolejnych liczb całkowitych jest podzielny przez 2 i 3.

