/Szkoła średnia/Liczby/Liczby całkowite/Podzielność/1 literka

Zadanie nr 8209684

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla każdej liczby naturalnej 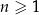n ≥ 1 liczba 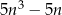3 5n − 5n jest podzielna przez 30.

Rozwiązanie

Ponieważ

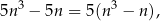
5n3 − 5n = 5(n3 − n),

wystarczy udowodnić, że liczba 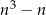n3 − n dzieli się przez 6. Zauważmy, że

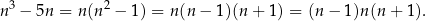
3 2 n − 5n = n (n − 1) = n(n − 1 )(n+ 1) = (n − 1)n (n+ 1).

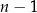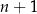Ponieważ jest to iloczyn trzech kolejnych liczb naturalnych, to liczba ta jest podzielna przez 3 (bo jedna z liczb: n − 1 , n lub n + 1 dzieli się przez 3). Ponadto, 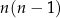n(n − 1) jest liczbą parzystą jako iloczyn dwóch kolejnych liczb naturalnych. Całe wyrażenie dzieli się więc przez 6.

Wersja PDF