Zadanie nr 9126821
Wykaż, że liczba 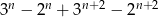 jest podzielna przez 10,
jest podzielna przez 10, 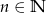 .
.
Rozwiązanie
Przekształcamy dane wyrażenie
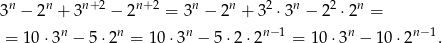
Widać teraz, że oba składniki dzielą się przez 10.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że liczba 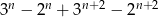 jest podzielna przez 10,
jest podzielna przez 10, 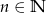 .
.
Przekształcamy dane wyrażenie
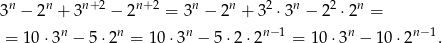
Widać teraz, że oba składniki dzielą się przez 10.
