Zadanie nr 9425403
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 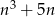 jest podzielna przez 6.
jest podzielna przez 6.
Rozwiązanie
Sposób I
Zapiszmy dane wyrażenie w postaci
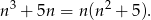
Zauważmy najpierw, że powyższa liczba na pewno jest parzysta: albo  jest parzyste, albo parzysta jest liczba
jest parzyste, albo parzysta jest liczba 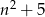 .
.
Wystarczy zatem wykazać, że liczba ta dzieli się przez 3. Jeżeli  dzieli się przez 3, to sprawa jest oczywista, więc załóżmy, że
dzieli się przez 3, to sprawa jest oczywista, więc załóżmy, że 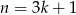 lub
lub 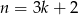 . Mamy wtedy odpowiednio
. Mamy wtedy odpowiednio
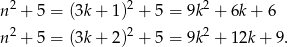
W obu przypadkach liczba 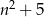 dzieli się przez 3, więc rzeczywiście liczba
dzieli się przez 3, więc rzeczywiście liczba 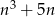 dzieli się przez 6.
dzieli się przez 6.
Sposób II
Zauważmy, że
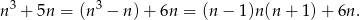
Zauważmy teraz, że pierwszy składnik tej sumy jest iloczynem trzech kolejnych liczb całkowitych, wśród których musi być liczba parzysta oraz liczba podzielna przez 3. Zatem 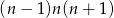 jest liczbą podzielną przez 6. Drugi składnik sumy:
jest liczbą podzielną przez 6. Drugi składnik sumy: 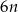 też oczywiście dzieli się przez 6, co kończy dowód.
też oczywiście dzieli się przez 6, co kończy dowód.

