Zadanie nr 5786396
Udowodnij, że dla każdej liczby całkowitej 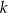 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 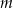 liczba
liczba 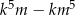 jest podzielna przez 10.
jest podzielna przez 10.
Rozwiązanie
Sposób I
Zauważmy, że
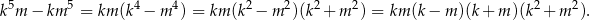
Widać teraz, że liczba ta jest parzysta, bo albo jedna z liczb 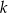 lub
lub 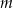 jest parzysta, albo
jest parzysta, albo 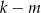 jest parzyste.
jest parzyste.
Zastanówmy się nad podzielnością przez 5. Jeżeli jedna z liczb 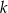 lub
lub 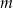 dzieli się przez 5, to podzielny przez 5 jest też iloczyn
dzieli się przez 5, to podzielny przez 5 jest też iloczyn 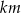 . Jeżeli liczby
. Jeżeli liczby 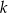 i
i 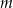 dają takie same reszty z dzielenia przez 5, to
dają takie same reszty z dzielenia przez 5, to 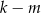 dzieli się przez 5. Podobnie, jeżeli reszty z dzielenia
dzieli się przez 5. Podobnie, jeżeli reszty z dzielenia 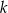 i
i 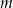 przez 5 to 1 i 4 lub 2 i 3 (w jakiejkolwiek kolejności), to przez 5 dzieli się
przez 5 to 1 i 4 lub 2 i 3 (w jakiejkolwiek kolejności), to przez 5 dzieli się 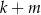 .
.
Wciąż zostały do sprawdzenia 4 przypadki reszt: 1 i 2, 1 i 3, 2 i 4, 3 i 4. Jeżeli oznaczymy 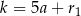 i
i 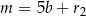 , gdzie
, gdzie 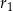 i
i 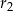 są jedną z czterech wymienionych par reszt, to mamy kolejno
są jedną z czterech wymienionych par reszt, to mamy kolejno
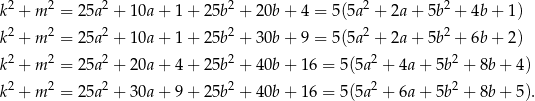
W każdej z tych sytuacji suma 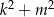 dzieli się przez 5. Zatem rzeczywiście liczba
dzieli się przez 5. Zatem rzeczywiście liczba 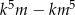 zawsze dzieli się przez
zawsze dzieli się przez 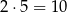 .
.
Sposób II
Parzystość liczby
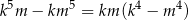
uzasadniamy tak samo jak w poprzednim sposobie. Tak samo też uzasadniamy podzielność przez 5, jeżeli jedna z liczb 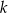 lub
lub 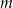 dzieli się przez 5. Zauważmy ponadto, że
dzieli się przez 5. Zauważmy ponadto, że
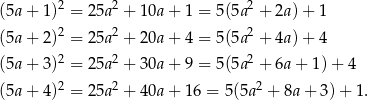
To oznacza, że kwadrat liczby całkowitej, która nie jest podzielna przez 5 zawsze daje resztę 1 lub 4 przy dzieleniu przez 5. W szczególności, jeżeli 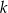 i
i 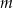 nie dzielą się przez 5, to liczba
nie dzielą się przez 5, to liczba
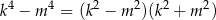
zawsze dzieli się przez 5 – tak jest, bo albo 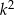 i
i 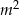 dają te same reszty z dzielenia przez 5, albo dają reszty 1 i 4 (w pewnej kolejności). Zatem rzeczywiście liczba
dają te same reszty z dzielenia przez 5, albo dają reszty 1 i 4 (w pewnej kolejności). Zatem rzeczywiście liczba
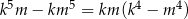
zawsze dzieli się przez 10.

