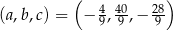Zadanie nr 1609944
Wykresem funkcji kwadratowej 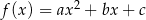 jest parabola styczna do prostej
jest parabola styczna do prostej 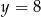 w punkcie
w punkcie 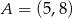 oraz przechodząca przez punkt
oraz przechodząca przez punkt 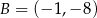 . Wyznacz wartości współczynników
. Wyznacz wartości współczynników 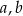 i
i  .
.
Rozwiązanie
Podany punkt styczności 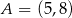 paraboli z poziomą prostą musi być wierzchołkiem tej paraboli. To oznacza, że parabola ta ma postać kanoniczną
paraboli z poziomą prostą musi być wierzchołkiem tej paraboli. To oznacza, że parabola ta ma postać kanoniczną
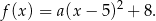
Współczynnik  wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 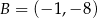 .
.
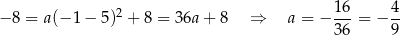
Stąd
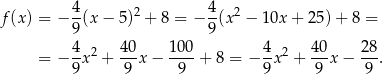
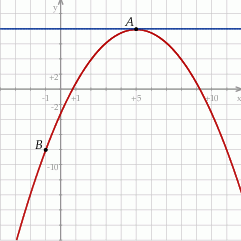
Na koniec wykres dla ciekawskich.
Odpowiedź: