Zadanie nr 4851171
Funkcja kwadratowa 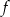 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu 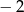 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 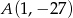 . Napisz wzór funkcji
. Napisz wzór funkcji 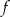 w postaci ogólnej.
w postaci ogólnej.
Rozwiązanie
Skoro funkcja 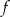 ma tylko jedno miejsce zerowe to musi być pełnym kwadratem, czyli ma wzór postaci
ma tylko jedno miejsce zerowe to musi być pełnym kwadratem, czyli ma wzór postaci
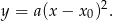
Wiemy ponadto, że przyjmuje największą wartość, czyli jej ramiona muszą być skierowane w dół. W takiej sytuacji największą wartość przyjmuje w wierzchołku, czyli 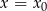 . Zatem
. Zatem 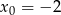 i szukamy wzoru postaci
i szukamy wzoru postaci
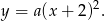
Współczynnik  wyznaczamy podstawiając współrzędne danego punktu
wyznaczamy podstawiając współrzędne danego punktu 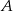 .
.
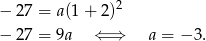
Zatem
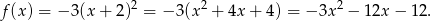
Na koniec obrazek dla ciekawskich.
Odpowiedź: