/Szkoła średnia/Funkcje/Kwadratowa/Wyznacz wzór

Zadanie nr 9075828

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja kwadratowa 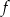f ma następujące własności:
– zbiorem wartości funkcji 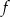f jest przedział (− ∞ ,8⟩ ;
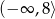– funkcja 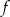f jest rosnąca w przedziale 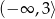(− ∞ ,3⟩ i malejąca w przedziale ⟨3,+ ∞ ) ;
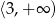– wykres funkcji 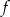f przecina oś 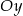Oy w punkcie, którego rzędna jest równa (− 10) .
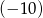Wyznacz wzór funkcji 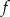f w postaci iloczynowej.

Rozwiązanie

Szukamy funkcji 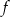f w postaci kanonicznej

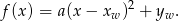
2 f(x) = a (x− xw) + yw .

Skoro zbiorem wartości funkcji 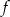f jest przedział 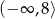(− ∞ ,8⟩ , ramiona paraboli będącej wykresem tej funkcji muszą być skierowane w dół (czyli 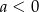a < 0 ), oraz druga współrzędna wierzchołka musi być równa y = 8 w .

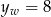Z informacji o przedziałach monotoniczności funkcji 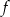f wynika, że pierwsza współrzędna wierzchołka paraboli będącej jej wykresem jest równa xw = 3 .

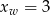Wiemy więc, że funkcja 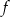f ma postać

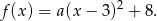
f (x) = a(x − 3)2 + 8.

Pozostało teraz wykorzystać ostatnią informację, czyli równość 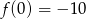f(0) = − 10 .

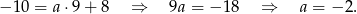
− 1 0 = a⋅ 9+ 8 ⇒ 9a = − 18 ⇒ a = − 2.

Mamy więc (korzystamy ze wzoru skróconego mnożenia na różnicę kwadratów)

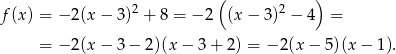
2 ( 2 ) f(x) = − 2(x− 3) + 8 = − 2 (x− 3) − 4 = = − 2(x− 3− 2)(x− 3+ 2) = − 2(x − 5)(x − 1).

 
Odpowiedź: f(x ) = − 2(x − 5)(x − 1)

Wersja PDF