Po wyrzuceniu ze szkoły pochodnych, funkcja kwadratowa stała się tematem przewodnim wszystkich zadań na ekstrema. Sytuacja jest w zasadzie dość prosta – zadania tego typu sprowadzają się do wyznaczenia najmniejszej/największej wartości funkcji kwadratowej na pewnym przedziale. Możliwe konfiguracje są następujące.
-
Jeżeli szukamy wartości największej, ramiona paraboli są skierowane w dół i wierzchołek jest zawarty w rozważanym przedziale,
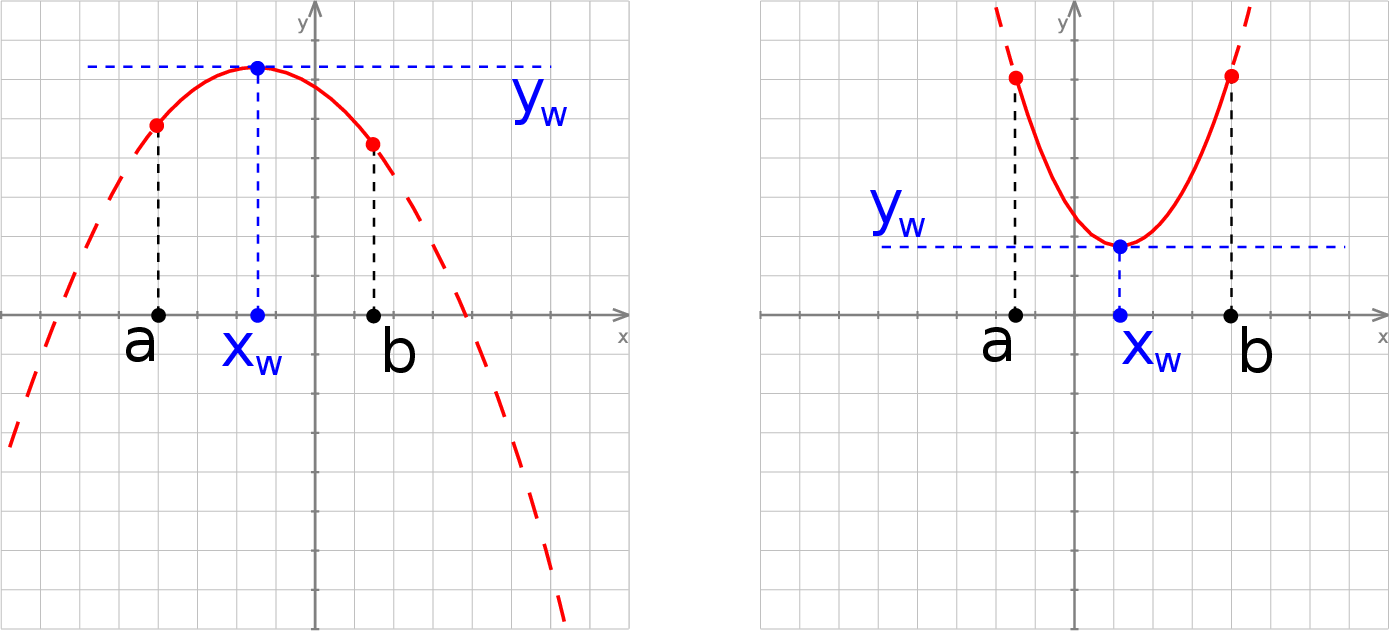
to wartość największa jest osiągana w wierzchołku, to znaczy
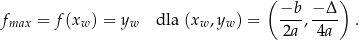
-
Jeżeli szukamy wartości najmniejszej, ramiona paraboli są skierowane do góry i wierzchołek jest zawarty w rozważanym przedziale, to wartość najmniejsza jest osiągana w wierzchołku.
-
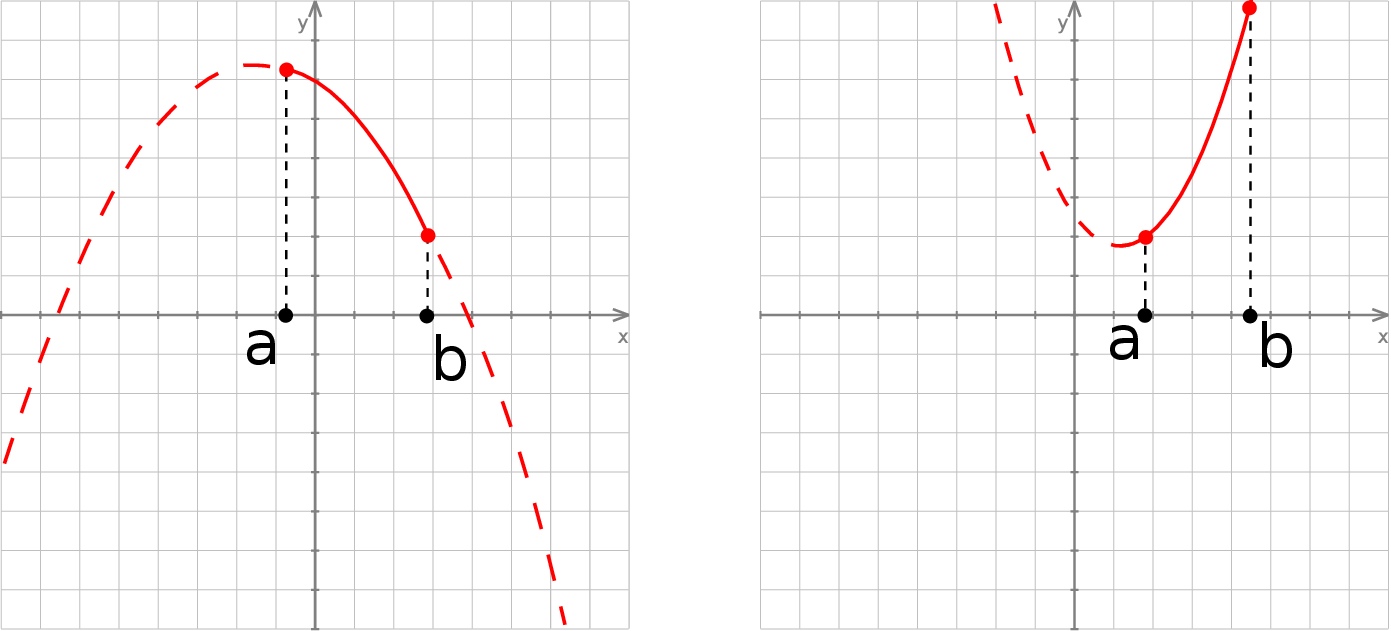
W każdej innej sytuacji, wartość największa/najmniejsza jest osiągana w jednym z końców przedziału. W którym? – trzeba policzyć wartości w obu końcach i je porównać.
Znajdźmy najmniejszą wartość funkcji
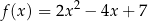
na przedziale 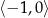 .
.
Ponieważ 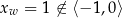 , wartość ta jest przyjmowana w jednym z końców przedziału. Mamy
, wartość ta jest przyjmowana w jednym z końców przedziału. Mamy
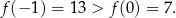
Zatem najmniejsza wartość to 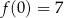 .
.
Ważna jest dziedzina! W zadaniach na ekstrema bardzo ważne (i często kłopotliwe) jest wyznaczenie przedziału, na którym szukamy ekstremum. Ogólna zasada jest taka, że gdy wyznaczymy już wzór funkcji 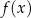 , której mamy znaleźć ekstremum, to musimy ustalić jakie są możliwe wartości argumentu
, której mamy znaleźć ekstremum, to musimy ustalić jakie są możliwe wartości argumentu  . Jak to zrobić? – to zależy od rodzaju i treści zadania: jeżeli
. Jak to zrobić? – to zależy od rodzaju i treści zadania: jeżeli  jest długością jakiegoś odcinka to
jest długością jakiegoś odcinka to 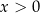 , jeżeli
, jeżeli 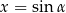 to
to 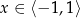 , jeżeli
, jeżeli 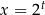 to
to 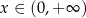 itd.
itd.
Spróbujmy znaleźć największe możliwe pole prostokąta o obwodzie 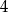 .
.
Jeżeli oznaczymy boki prostokąta przez  i
i 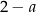 , to szukamy największej możliwej wartości wyrażenia
, to szukamy największej możliwej wartości wyrażenia 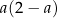 . Na jakim przedziale? – boki prostokąta nie mogą być ujemne, więc
. Na jakim przedziale? – boki prostokąta nie mogą być ujemne, więc 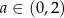 . Łatwo policzyć, że maksymalne pole mamy dla kwadratu o boku 1.
. Łatwo policzyć, że maksymalne pole mamy dla kwadratu o boku 1.
Z krawędzi dachu podrzucono kamień, który po 2 sekundach spadł na ziemię. Wysokość, na jakiej znajdował się kamień nad ziemią po upływie 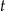 sekund od chwili jego podrzucenia, opisuje funkcja
sekund od chwili jego podrzucenia, opisuje funkcja 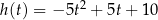 . Na jaką największą wysokość wzniósł się ten kamień?
. Na jaką największą wysokość wzniósł się ten kamień?
Na jakim przedziale szukamy maksimum funkcji 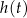 – na takim, jak zmienia się czas, czyli dla
– na takim, jak zmienia się czas, czyli dla 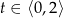 .
.

