/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem/1 literka

Zadanie nr 3154524

Napisz wzór i narysuj wykres funkcji 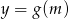y = g(m ) , która każdej liczbie rzeczywistej 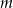m przyporządkowuje najmniejszą wartość funkcji kwadratowej 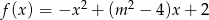f (x) = −x 2 + (m 2 − 4 )x+ 2 w przedziale ⟨− 1,1⟩ .

Wersja PDF

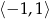Rozwiązanie

Wykresem funkcji 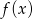f(x ) jest parabola o ramionach skierowanych w dół, więc przyjmuje wartość najmniejszą w przedziale 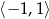⟨− 1,1⟩ w jednym z jego końców. Obliczmy wartości w końcach przedziału ⟨− 1,1⟩ .

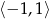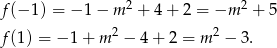
f(− 1) = −1 − m 2 + 4 + 2 = −m 2 + 5 2 2 f(1) = − 1+ m − 4 + 2 = m − 3.

Sprawdźmy, kiedy druga z tych liczb jest większa od pierwszej.

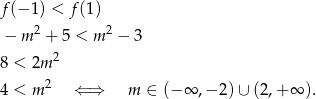
f (− 1) < f(1) − m 2 + 5 < m 2 − 3 2 8 < 2m 4 < m 2 ⇐ ⇒ m ∈ (−∞ ,− 2) ∪ (2,+ ∞ ).

Widać zatem, że wartość najmniejsza to

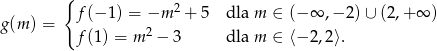
{ 2 g(m ) = f (− 1) = −m + 5 dla m ∈ (− ∞ ,− 2) ∪ (2,+ ∞ ) f (1) = m 2 − 3 dla m ∈ ⟨− 2,2 ⟩.

Teraz bez trudu szkicujemy wykres.

PIC

 
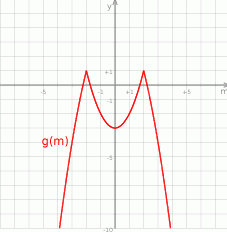
Odpowiedź: { −m 2 + 5 dla m ∈ (− ∞ ,− 2)∪ (2,+ ∞ ) g(m ) = 2 m − 3 dla m ∈ ⟨− 2,2⟩.

Wersja PDF