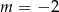/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem/1 literka

Zadanie nr 3248348

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź taką wartość parametru 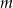m , aby największa wartość funkcji 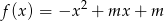f (x) = −x 2 + mx + m była najmniejsza z możliwych.

Rozwiązanie

Ponieważ wykresem podanej funkcji jest parabola o ramionach skierowanych w dół, więc jej największą wartością jest druga współrzędna wierzchołka, czyli

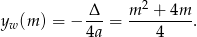
-Δ- m-2 +-4m- yw (m ) = − 4a = 4 .

Mamy zatem funkcję 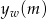yw(m ) , której wykres również jest parabolą, ale o ramionach skierowanych do góry. Wartość najmniejsza tej funkcji jest osiągana w pierwszej współrzędnej wierzchołka wykresu funkcji 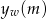yw (m ) . Zatem

−4 m = ---= − 2. 2

 
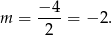
Odpowiedź: m = − 2

Wersja PDF