Zadanie nr 5643673
Funkcja kwadratowa 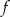 jest określona wzorem
jest określona wzorem 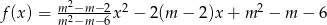 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 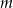 , dla których rozwiązaniem nierówności
, dla których rozwiązaniem nierówności 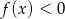 jest przedział postaci
jest przedział postaci 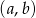 , gdzie
, gdzie 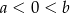 .
.
Rozwiązanie
Rozłóżmy najpierw trójmiany pojawiające się we wzorze funkcji 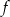 .
.
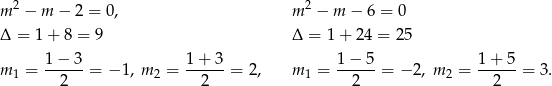
Zatem
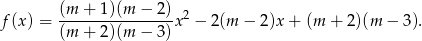
Ze względu na mianownik we wzorze musi oczywiście być 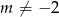 i
i 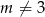 . Skoro rozwiązaniem nierówności
. Skoro rozwiązaniem nierówności 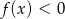 ma być przedział
ma być przedział 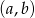 , to wykresem funkcji
, to wykresem funkcji 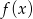 musi być parabola o ramionach kierowanych w górę, czyli współczynnik przy
musi być parabola o ramionach kierowanych w górę, czyli współczynnik przy 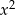 musi być dodatni. Mamy więc
musi być dodatni. Mamy więc
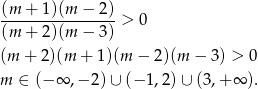
Sprawdźmy teraz, kiedy funkcja ma dwa miejsca zerowe.
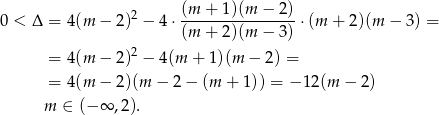
Przy tym założeniu możemy zapisać wzory Viète’a.
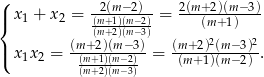
Informacja o tym, że rozwiązaniem nierówności 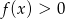 jest przedział
jest przedział 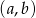 , gdzie
, gdzie 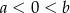 oznacza, że pierwiastki wielomianu
oznacza, że pierwiastki wielomianu 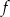 muszą mieć różne znaki, czyli musi być spełniona nierówność
muszą mieć różne znaki, czyli musi być spełniona nierówność 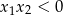 . Tak będzie, gdy
. Tak będzie, gdy
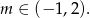
Łącząc wszystkie otrzymane warunki mamy
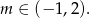
Odpowiedź: