/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem/1 literka

Zadanie nr 6462971

Dodaj do ulubionych
Dodaj do rozwiązanych

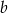Liczba b jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji 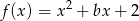f(x) = x 2 + bx + 2 jest większa od 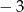− 3 . Wyznacz liczbę b .

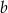Rozwiązanie

Wykresem podanej funkcji jest parabola o ramionach skierowanych do góry, więc najmniejszą wartość przyjmuje w wierzchołku i jest ona równa

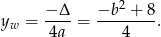
−-Δ- −b-2-+-8 yw = 4a = 4 .

Sprawdźmy kiedy jest ona większa od 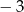− 3 .

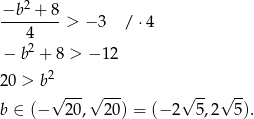
−b-2 +-8 4 > − 3 / ⋅ 4 2 − b + 8 > −1 2 20 > b2 √ ---√ --- √ -- √ -- b ∈ (− 20, 20) = (− 2 5,2 5).

Ponieważ 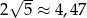√ -- 2 5 ≈ 4,47 , największą liczba całkowitą w tym przedziale jest 4.  
Odpowiedź: b = 4

Wersja PDF