/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem/1 literka

Zadanie nr 9071508

Dodaj do ulubionych
Dodaj do rozwiązanych

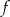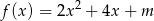Funkcję kwadratową f można opisać wzorem mającym postać f (x) = 2x2 + 4x + m .

  • Wyznacz warunek, dla którego funkcja 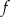f ma dwa różne pierwiastki 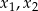x ,x 1 2 , a następnie oblicz x + x 1 2 .
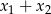  • Wiedząc dodatkowo, że 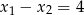x1 − x2 = 4 , oblicz 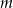m . Dla wyznaczonej liczby 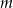m naszkicuj wykres funkcji 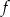f w układzie współrzędnych, a następnie rozwiąż równanie f(x − 3) = −6 .
    PIC

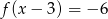Rozwiązanie

  • Sprawdzamy, kiedy Δ > 0 .
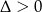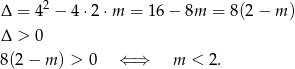
    Δ = 42 − 4 ⋅2⋅ m = 16− 8m = 8(2 − m ) Δ > 0 8 (2− m ) > 0 ⇐ ⇒ m < 2.

    Sumę pierwiastków obliczymy na dwa sposoby

    Sposób I

    Korzystamy ze wzorów Viète’a

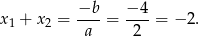
    −b-- −-4- x1 + x2 = a = 2 = − 2.

    Sposób II

    Korzystamy ze wzoru na pierwiastki trójmianu

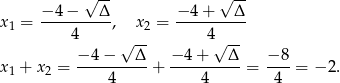
    √ -- √ -- −-4−----Δ- −-4-+---Δ- x 1 = 4 , x2 = 4 √ -- √ -- x 1 + x 2 = −-4−---Δ-+ −-4+----Δ-= −-8-= − 2. 4 4 4

     
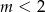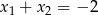
    Odpowiedź: m < 2 , x + x = −2 1 2

  • Rozwiązujemy układ równań
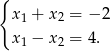
    { x1 + x2 = − 2 x − x = 4. 1 2

    Dodajemy stronami równania i otrzymujemy

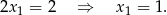
    2x = 2 ⇒ x = 1. 1 1

    Zatem 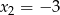x2 = − 3 . Skoro wiemy, że liczba 1 jest pierwiastkiem, mamy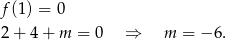

    f(1 ) = 0 2 + 4 + m = 0 ⇒ m = − 6.

    Mamy więc do czynienia z funkcją

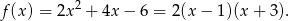
    2 f(x) = 2x + 4x − 6 = 2(x − 1 )(x+ 3).

    Wierzchołek paraboli będącej wykresem tej funkcji ma pierwszą współrzędną równą 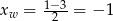x = 1−-3-= − 1 w 2 (dokładnie w środku między pierwiastkami), a drugą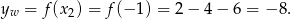

    yw = f (x2) = f(− 1) = 2− 4− 6 = − 8.

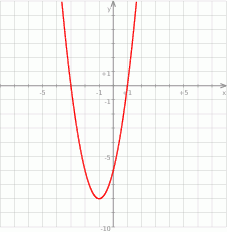
    Teraz możemy naszkicować wykres

    PIC

    Rozwiązujemy równanie

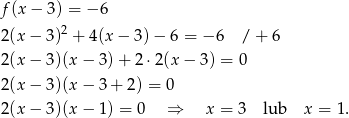
    f(x − 3) = − 6 2(x − 3)2 + 4(x − 3) − 6 = − 6 /+ 6 2(x − 3)(x − 3) + 2 ⋅2(x − 3) = 0 2(x − 3)(x − 3 + 2) = 0 2(x − 3)(x − 1) = 0 ⇒ x = 3 lub x = 1.

     
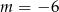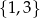    Odpowiedź: m = − 6 , rozwiązaniem równania jest zbiór {1,3} .

Wersja PDF