Zadanie nr 2094719
Funkcja kwadratowa 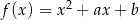 ma dwa miejsca zerowe, które różnią się o 7. Wykres funkcji
ma dwa miejsca zerowe, które różnią się o 7. Wykres funkcji 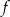 przechodzi przez punkt
przechodzi przez punkt 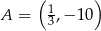 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 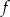 .
.
Rozwiązanie
Sposób I
Trójmian o pierwiastkach 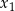 i
i 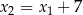 ma postać iloczynową
ma postać iloczynową
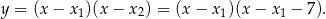
Podstawiamy współrzędne punktu 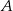 i wyznaczamy
i wyznaczamy 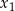
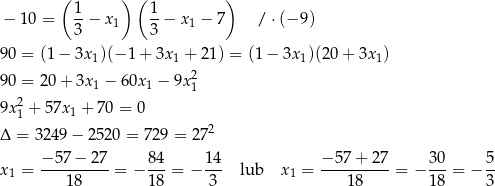
Wtedy 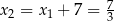 i
i 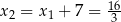 odpowiednio Zatem trójmian ma postać iloczynową
odpowiednio Zatem trójmian ma postać iloczynową
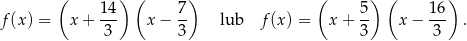
W obu przypadkach wykresem jest parabola o ramionach skierowanych do góry. Pierwsza współrzędna wierzchołka tej paraboli jest odpowiednio równa
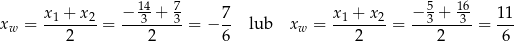
(wierzchołek zawsze znajduje się w środku pomiędzy pierwiastkami). W pierwszym przypadku najmniejsza wartość funkcji to
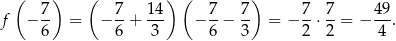
W drugim przypadku najmniejsza wartość funkcji to
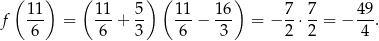
Na koniec wykresy obu funkcji.
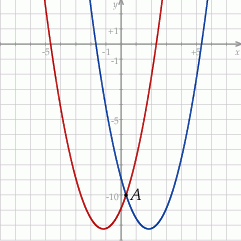
Sposób II
Niech 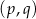 będzie wierzchołkiem paraboli będącej wykresem danej funkcji kwadratowej. Ponieważ pierwsza współrzędna wierzchołka paraboli znajduje się w środku między pierwiastkami, miejscami zerowymi funkcji
będzie wierzchołkiem paraboli będącej wykresem danej funkcji kwadratowej. Ponieważ pierwsza współrzędna wierzchołka paraboli znajduje się w środku między pierwiastkami, miejscami zerowymi funkcji 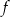 są liczby
są liczby 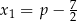 i
i 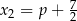 . Stąd na mocy wzorów Viète’a
. Stąd na mocy wzorów Viète’a
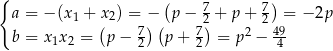
Korzystamy teraz ze wzoru z 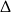 –ą na drugą współrzędną wierzchołka paraboli
–ą na drugą współrzędną wierzchołka paraboli
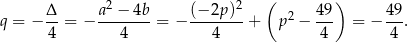
Zauważmy, że w tym sposobie nie korzystaliśmy z podanych współrzędnych punktu 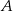 .
.
Odpowiedź: