Zadanie nr 6483930
Funkcja kwadratowa określona wzorem 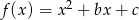 osiąga wartości ujemne wtedy i tylko wtedy, gdy
osiąga wartości ujemne wtedy i tylko wtedy, gdy 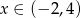 .
.
- Wyznacz wartości współczynników
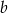 i
i  .
. - Oblicz, dla jakich argumentów
 , wartości funkcji
, wartości funkcji 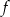 są mniejsze od wartości funkcji kwadratowej
są mniejsze od wartości funkcji kwadratowej 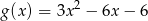 .
. - Rozwiąż równanie
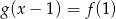 .
.
Rozwiązanie
- Z podanych informacji wynika, że miejscami zerowymi danej funkcji są liczby
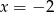 i
i 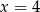 . Współczynniki
. Współczynniki 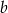 i
i  można wyliczyć wstawiając te liczby do wzoru, ze wzorów Viète’a lub z postaci iloczynowej. My zrobimy to tym ostatnim sposobem.
można wyliczyć wstawiając te liczby do wzoru, ze wzorów Viète’a lub z postaci iloczynowej. My zrobimy to tym ostatnim sposobem. 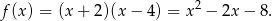
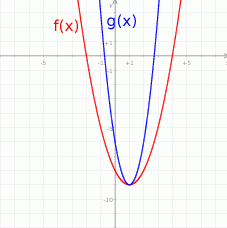
Odpowiedź: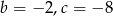
- Liczymy
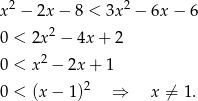
Odpowiedź: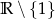
- Liczymy
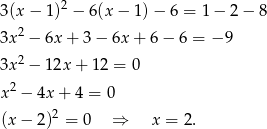
Odpowiedź: