/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem/2 literki

Zadanie nr 9737330

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wzór funkcji 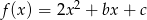2 f (x ) = 2x + bx + c w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania |x − 3| = 5 .

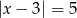Rozwiązanie

Sposób I

Rozwiążmy najpierw podane równanie

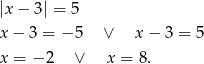
|x− 3| = 5 x − 3 = − 5 ∨ x − 3 = 5 x = − 2 ∨ x = 8.

Zatem szukana funkcja musi mieć postać

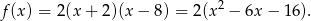
2 f(x) = 2 (x+ 2)(x− 8) = 2(x − 6x − 1 6).

Pozostało wyznaczyć postać kanoniczną.

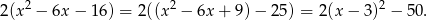
2 2 2 2(x − 6x − 16) = 2((x − 6x + 9)− 25) = 2(x − 3 ) − 50 .

Sposób II

Podnosimy dane równanie stronami do kwadratu

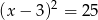
(x − 3)2 = 2 5

Zatem rozwiązania tego równania są miejscami zerowymi funkcji

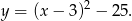
y = (x − 3)2 − 25.

Ponieważ szukamy funkcji ze współczynnikiem 2 przy 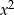x2 , musimy powyższy wzór pomnożyć przez 2, czyli

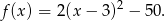
2 f(x) = 2 (x − 3) − 5 0.

 
Odpowiedź: f (x) = 2(x − 3)2 − 50

Wersja PDF