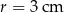/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Różne

Zadanie nr 5388103

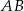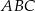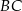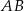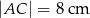Bok AB trójkąta ABC jest średnicą okręgu opisanego na tym trójkącie. Bok BC jest o 2 cm krótszy od boku AB oraz |AC | = 8 cm . Oblicz pole trójkąta 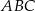ABC oraz długość promienia okręgu wpisanego w ten trójkąt.

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

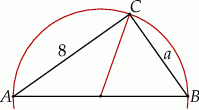
Zauważmy najpierw, że kąt 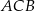ACB jest oparty na średnicy okręgu, więc 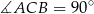∡ACB = 90∘ i trójkąt 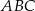ABC jest prostokątny. Jeżeli oznaczymy 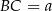BC = a , to wiemy, że 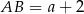AB = a + 2 i twierdzenie Pitagorasa prowadzi do równania

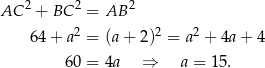
AC 2 + BC 2 = AB 2 2 2 2 64+ a = (a + 2) = a + 4a + 4 60 = 4a ⇒ a = 15.

Stąd 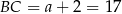BC = a + 2 = 1 7 . Pole trójkąta jest równe

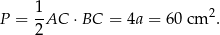
1- 2 P = 2AC ⋅BC = 4a = 60 cm .

Promień okręgu wpisanego obliczymy na dwa sposoby.

Sposób I

Korzystamy ze wzoru na pole

P = pr,

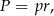
gdzie

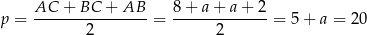
AC + BC + AB 8 + a + a + 2 p = ---------------- = ------------- = 5+ a = 20 2 2

jest połową obwodu trójkąta. Mamy zatem

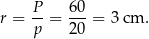
P 60 r = p-= 20-= 3 cm .

Sposób II

Tym razem skorzystamy ze wzoru

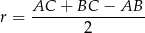
AC--+--BC-−-AB-- r = 2

na promień okręgu wpisanego w trójkąt prostokątny. W naszej sytuacji mamy

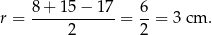
8+--15−--17- 6- r = 2 = 2 = 3 cm .

 
Odpowiedź: 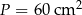P = 60 cm 2 , r = 3 cm

Wersja PDF