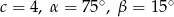/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Różne

Zadanie nr 7904110

Wyznacz długość przeciwprostokątnej oraz miary kątów trójkąta prostokątnego, którego przyprostokątne mają długości 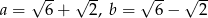√ -- √ -- √ -- √ -- a = 6+ 2, b = 6− 2 .

Wersja PDF

Rozwiązanie

Możemy zacząć od szkicowego rysunku.

PIC

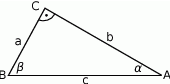
Długość przeciwprostokątnej wyliczamy z twierdzenia Pitagorasa.

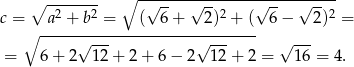
∘ ------- ∘ -√-----√--------√-----√---- c = a2 + b2 = ( 6+ 2)2 + ( 6− 2)2 = ∘ ------------------------------ = 6 + 2√ 1-2+ 2 + 6 − 2√ 12+ 2 = √ 16-= 4 .

Stąd

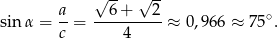
√ -- √ -- a- --6+----2- ∘ sinα = c = 4 ≈ 0,9 66 ≈ 75 .

Tak się składa, że jesteśmy w stanie policzyć dokładną wartość 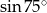sin 75∘ ze wzoru na sinus sumy

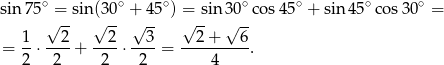
sin 75∘ = sin (30∘ + 45∘) = sin 30∘co s45∘ + sin45 ∘cos 30∘ = √ -- √ -- √ -- √ -- √ -- 1- --2- ---2 --3- --2+----6- = 2 ⋅ 2 + 2 ⋅ 2 = 4 .

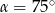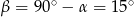Zatem α = 75 ∘ dokładnie, a nie w przybliżeniu. Stąd β = 90 ∘ − α = 15∘ .  
Odpowiedź: c = 4 , α = 7 5∘, β = 15∘

Wersja PDF