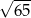/Szkoła średnia/Funkcje/Kwadratowa/Z parametrem/3 literki

Zadanie nr 3418702

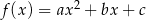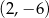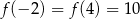Parabola, która jest wykresem funkcji kwadratowej 2 f (x) = ax + bx + c , przechodzi przez punkt (2,− 6) oraz f(− 2) = f (4) = 10 . Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.

Wersja PDF

Rozwiązanie

Sposób I

Wiemy, że miejscami zerowymi funkcji 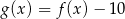g(x) = f (x)− 10 są liczby 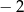− 2 i 4, więc ma ona wzór postaci

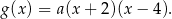
g(x ) = a(x + 2)(x − 4).

Zatem

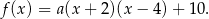
f(x) = a(x + 2 )(x− 4)+ 10.

Współczynnik a obliczamy podstawiając współrzędne podanego punktu na wykresie.

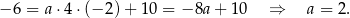
− 6 = a ⋅4⋅(− 2 )+ 10 = − 8a+ 10 ⇒ a = 2 .

Z podanej informacji 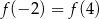f (− 2) = f(4) wiemy, że osią symetrii wykresu funkcji 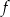f jest prosta 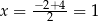−2+4 x = --2--= 1 , czyli taka jest pierwsza współrzędna wierzchołka tej paraboli. Obliczmy jeszcze drugą współrzędną wierzchołka

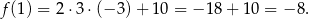
f(1) = 2 ⋅3 ⋅(− 3)+ 10 = − 18 + 10 = −8 .

Wierzchołek ma więc współrzędne 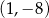(1,− 8) i jego odległość od początku układu współrzędnych jest równa

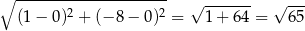
∘ --------------------- √ ------- √ --- (1 − 0)2 + (− 8 − 0)2 = 1 + 64 = 65

Sposób II

Z podanej informacji 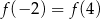f(− 2) = f(4) wiemy, że osią symetrii wykresu funkcji 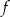f jest prosta 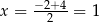−2+4 x = --2--= 1 , czyli taka jest pierwsza współrzędna wierzchołka tej paraboli. Wzór funkcji 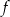f możemy więc zapisać w postaci kanonicznej

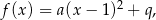
f (x) = a(x − 1)2 + q,

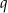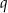gdzie q jest drugą współrzędną wierzchołka paraboli. Współczynniki a i q obliczamy podstawiając współrzędne punktów 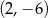(2,− 6) oraz (− 2,10 ) .

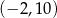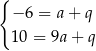
{ − 6 = a + q 10 = 9a + q

Jeżeli odejmiemy od drugiego równania pierwsze, to mamy 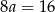8a = 16 , czyli 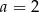a = 2 . Stąd 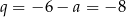q = − 6 − a = − 8 i wierzchołek paraboli ma współrzędne 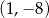(1,− 8) . Jego odległość od początku układu współrzędnych obliczamy tak samo jak w pierwszym sposobie.

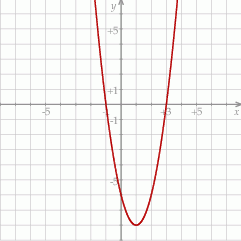
Na koniec wykres dla ciekawskich.

PIC

 
Odpowiedź: √ --- 65

Wersja PDF