Zadanie nr 8163916
Funkcja kwadratowa 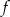 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 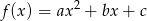 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 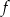 jest równa
jest równa 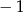 oraz
oraz 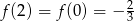 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
.
Rozwiązanie
Sposób I
Wiemy, że liczby 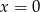 i
i 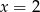 są miejscami zerowymi funkcji
są miejscami zerowymi funkcji 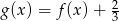 . To oznacza, że funkcja
. To oznacza, że funkcja 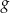 ma postać
ma postać
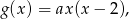
czyli
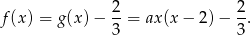
Wiemy ponadto, że funkcja ta przyjmuje wartość najmniejszą, więc 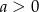 (ramiona paraboli muszą być skierowane w górę). W takiej sytuacji funkcja
(ramiona paraboli muszą być skierowane w górę). W takiej sytuacji funkcja 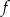 przyjmuje wartość najmniejszą dokładnie w środku między pierwiastkami funkcji
przyjmuje wartość najmniejszą dokładnie w środku między pierwiastkami funkcji 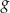 , czyli dla
, czyli dla
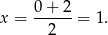
Mamy zatem
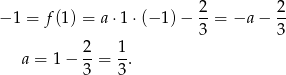
Sposób II
Jeżeli parabola będąca wykresem funkcji 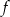 ma przyjmować wartość najmniejszą, to jej ramiona muszą być skierowane w górę. Znamy ponadto dwa punkty, w których funkcja ta przyjmuje tę samą wartość, więc możemy obliczyć pierwszą współrzędną jej wierzchołka
ma przyjmować wartość najmniejszą, to jej ramiona muszą być skierowane w górę. Znamy ponadto dwa punkty, w których funkcja ta przyjmuje tę samą wartość, więc możemy obliczyć pierwszą współrzędną jej wierzchołka
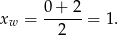
Funkcja 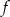 ma więc postać kanoniczną
ma więc postać kanoniczną
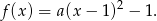
Współczynnik  obliczamy podstawiając współrzędne punktu
obliczamy podstawiając współrzędne punktu 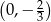 .
.
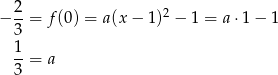
Sposób III
Podstawiamy we wzorze funkcji 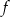 współrzędne punktów
współrzędne punktów 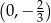 i
i 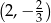 .
.
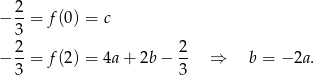
Funkcja 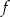 ma więc postać
ma więc postać
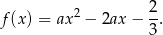
Pierwsza współrzędna wierzchołka paraboli będącej jej wykresem jest więc równa
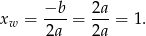
Mamy więc
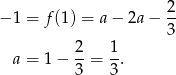
Na koniec wykres funkcji 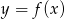 .
.
Odpowiedź: