/Szkoła podstawowa/Zadania testowe/Geometria/Trapez

Zadanie nr 6081837

Prosta 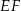EF dzieli trapez równoramienny 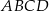ABCD na romb 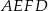AEF D o obwodzie 52 cm i trapez 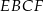EBCF o obwodzie o 13 cm mniejszym od obwodu rombu AEF D .

PIC

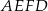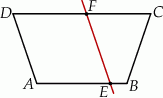
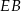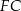Suma długości odcinków EB i F C jest równa
A) 14 cm B) 13 cm C) 15 cm D) 18 cm

Wersja PDF

Rozwiązanie

Jeżeli obwód rombu 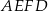AEF D jest równy 52 cm, to bok tego rombu ma długość 13 cm. Wiemy ponadto, że trapez 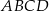ABCD jest równoramienny, więc 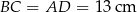BC = AD = 1 3 cm . Obwód trapezu 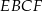EBCF jest równy

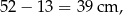
5 2− 13 = 39 cm ,

więc

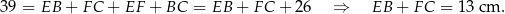
39 = EB + F C + EF + BC = EB + FC + 26 ⇒ EB + FC = 13 cm .

 
Odpowiedź: B

Wersja PDF