/Szkoła podstawowa/Zadania testowe/Geometria/Czworokąty

Zadanie nr 4212783

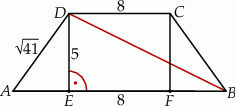
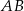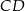Na rysunku przedstawiono trapez równoramienny o podstawach AB i CD . Dane są długości odcinków √ --- |AD | = 41 , |CD | = 8 , |DE | = 5 .

PIC

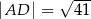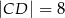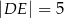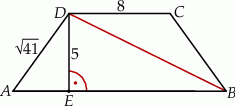
Długość przekątnej 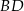BD jest równa
A) 13 B) 14 C) 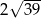√ --- 2 39 D) √ 89-

Wersja PDF

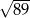
Rozwiązanie

Dorysujmy drugą wysokość 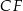CF trapezu.

PIC

Z twierdzenia Pitagorasa w trójkącie 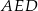AED mamy

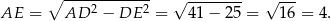
∘ ------------ √ -------- √ --- AE = AD 2 − DE 2 = 41 − 25 = 16 = 4.

Stąd

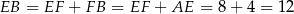
EB = EF + F B = EF + AE = 8+ 4 = 12

i z twierdzenia Pitagorasa w trójkącie 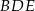BDE mamy

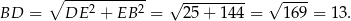
∘ ------------ √ --------- √ ---- BD = DE 2 + EB 2 = 25 + 144 = 169 = 13 .

 
Odpowiedź: A

Wersja PDF