Zadanie nr 1218894
Na okręgu o promieniu 3 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 12. Oblicz obwód tego trójkąta.
Rozwiązanie
Szkicujemy trójkąt prostokątny.
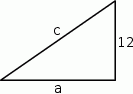
Korzystamy ze wzoru
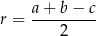
na promień  okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości
okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości  i
i 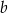 oraz przeciwprostokątnej długości
oraz przeciwprostokątnej długości  . Jeżeli oznaczymy
. Jeżeli oznaczymy 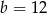 , to mamy
, to mamy
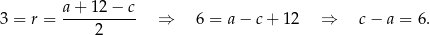
Ponadto, na mocy twierdzenia Pitagorasa
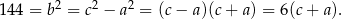
Mamy zatem
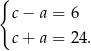
Jeżeli teraz odejmiemy od drugiego równania pierwsze (żeby skrócić  ), to mamy
), to mamy
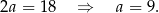
Stąd 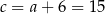 i obwód trójkąta
i obwód trójkąta  jest równy
jest równy
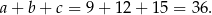
Odpowiedź: 36

