Zadanie nr 1446145
Na okręgu o promieniu 1 opisano trójkąt prostokątny, którego przyprostokątne mają długości  i
i 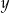 .
.
- Wyznacz
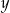 jako funkcję
jako funkcję  i określ dziedzinę tej funkcji.
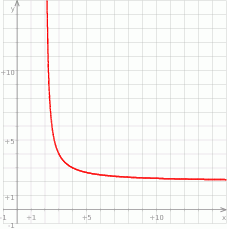
i określ dziedzinę tej funkcji. - Sporządź wykres tej funkcji.
Rozwiązanie
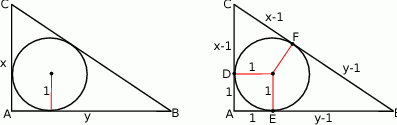
Rozpoczynamy od szkicowego rysunku.
-
Sposób I
Ze wzoru
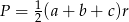 mamy
mamy 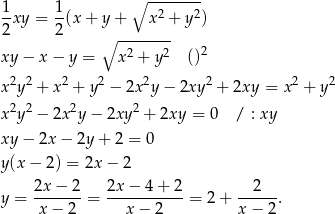
Dziedziną tej funkcji jest przedział
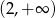 (inaczej półprosta
(inaczej półprosta 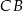 nie przecina prostej
nie przecina prostej 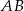 ).
). Sposób II
Niech
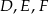 będą punktami styczności okręgu wpisanego z bokami trójkąta. Wtedy
będą punktami styczności okręgu wpisanego z bokami trójkąta. Wtedy 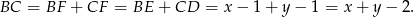
Piszemy teraz twierdzenie Pitagorasa.
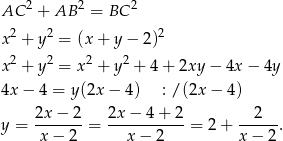
Dziedziną tej funkcji jest przedział
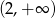 (bo musi być:
(bo musi być: 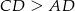 ).
).
Odpowiedź: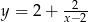 , dziedzina:
, dziedzina: 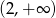 .
. - Z poprzedniego podpunktu wiemy, że jest to hiperbola
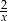 przesunięta o wektor
przesunięta o wektor ![[2,2]](https://img.zadania.info/zad/1446145/HzadR14x.gif) i obcięta do przedziału
i obcięta do przedziału 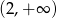 .
.