/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 1767380

Dodaj do ulubionych
Dodaj do rozwiązanych

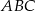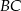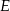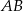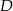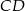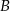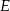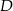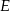Dany jest trójkąt prostokątny ABC , w którym przyprostokątna BC ma długość 6. Punkt E jest środkiem przeciwprostokątnej AB , spodek D wysokości CD leży między punktami B i E , a odległość między punktami D i E jest równa 7 (zobacz rysunek).

PIC

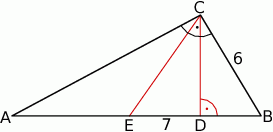
Oblicz obwód trójkąta 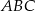ABC .

Rozwiązanie

Jeżeli oznaczymy 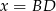x = BD , to

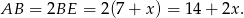
AB = 2BE = 2(7 + x) = 14+ 2x.

Korzystamy teraz z podobieństwa trójkątów 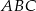ABC i CBD .

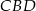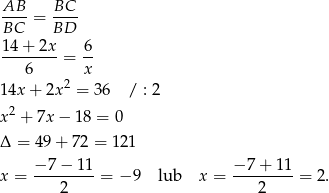
AB BC ----= ---- BC BD 14+--2x- 6- 6 = x 2 1 4x+ 2x = 36 / : 2 x 2 + 7x − 18 = 0 Δ = 49 + 72 = 121 −-7-−-11- −-7-+-11- x = 2 = − 9 lub x = 2 = 2.

Ujemne rozwiązanie odrzucamy i mamy 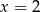x = 2 , czyli

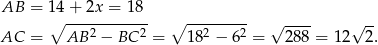
AB = 14 + 2x = 1 8 ∘ ---2------2- ∘ --2----2- √ ---- √ -- AC = AB − BC = 18 − 6 = 288 = 12 2.

Obwód trójkąta 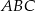ABC jest równy

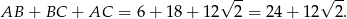
√ -- √ -- AB + BC + AC = 6+ 18 + 12 2 = 24+ 12 2.

 
Odpowiedź: √ -- 24 + 12 2

Wersja PDF