/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 1796252

Dodaj do ulubionych
Dodaj do rozwiązanych

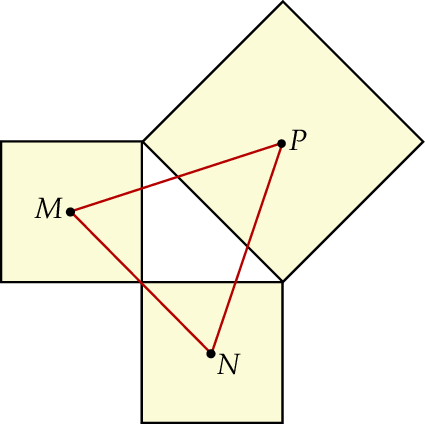
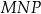Na zewnątrz równoramiennego trójkąta prostokątnego o przyprostokątnych równych a zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt MNP . Wykaż, że pole trójkąta MNP jest równe 2 a .

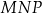ZINFO-FIGURE

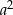Rozwiązanie

Oznaczmy przez 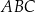ABC wierzchołki danego trójkąta prostokątnego (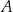A – wierzchołek kąta prostego). Ponadto niech 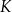K będzie środkiem przeciwprostokątnej.

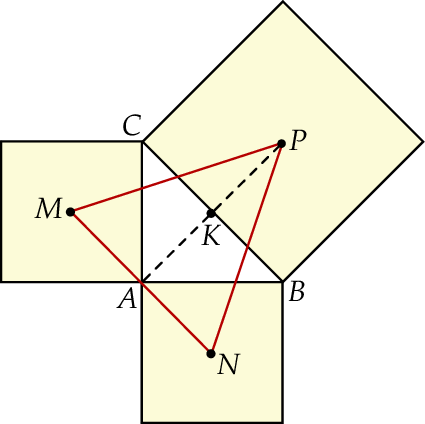
ZINFO-FIGURE

Zauważmy, trójkąt 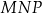MNP jest równoramienny, więc odcinek 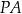PA jest jego wysokością. Łatwo obliczyć jej długość:

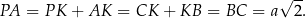
√ -- PA = P K + AK = CK + KB = BC = a 2.

Podstawa 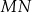MN trójkąta 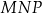MNP ma długość równą przekątnej mniejszego z kwadratów, zatem

√ -- MN = a 2 .

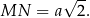
Pole trójkąta 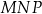MNP jest więc równe

√ -- √ -- 1MN ⋅PA = 1-⋅a 2⋅a 2 = a2. 2 2
Wersja PDF