/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 2004138

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie 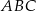ABC długość boku 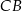CB stanowi 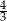4 3 długości boku 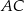AC , a kąt 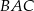BAC ma miarę 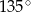135∘ . Oblicz cosinus kąta ABC .

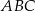Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

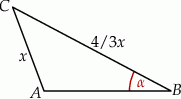
Będziemy chcieli skorzystać z twierdzenia sinusów, ale zanim to zrobimy, obliczmy

√ -- ∘ ∘ ∘ ∘ --2- sin1 35 = sin(180 − 45 ) = sin 45 = 2 .

Piszemy teraz twierdzenie sinusów w trójkącie 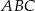ABC .

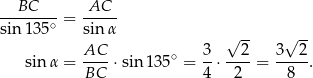
--BC----= -AC-- sin 135∘ sinα AC 3 √ 2- 3 √ 2- sinα = ----⋅sin 135∘ = --⋅ ----= -----. BC 4 2 8

Wiemy, że kąt 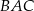BAC jest rozwarty, więc pozostałe kąty trójkąta są ostre. Zatem

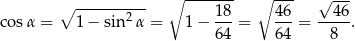
∘ ---------- ∘ ------- ∘ --- √ --- cosα = 1− sin 2α = 1 − 18-= 4-6 = --46-. 64 6 4 8

 
Odpowiedź: √ -- --46 8

Wersja PDF