Zadanie nr 2241465
W trójkącie 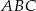 proste zawierające dwusieczne kątów poprowadzonych z wierzchołków
proste zawierające dwusieczne kątów poprowadzonych z wierzchołków 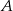 i
i 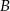 przecinają się pod kątem
przecinają się pod kątem 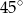 . Wiedząc, że
. Wiedząc, że 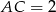 i
i 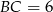 , oblicz
, oblicz
- długość boku
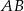 trójkąta
trójkąta 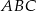 ;
; - długość środkowej trójkąta
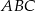 poprowadzonej z wierzchołka
poprowadzonej z wierzchołka 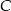 .
.
Rozwiązanie
Robimy rysunek.
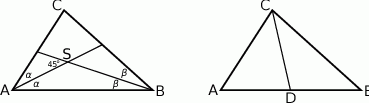
- Pierwszy problem jaki napotykamy, to gdzie zaznaczyć podany kąt
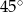 ? – są dwa kąty między prostymi
? – są dwa kąty między prostymi 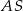 i
i 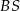 (w sumie dają
(w sumie dają 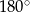 ) i musimy wiedzieć, o który z nich chodzi. Ponieważ jednak
) i musimy wiedzieć, o który z nich chodzi. Ponieważ jednak 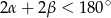
(suma dwóch kątów w trójkącie), więc
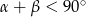 , czyli kąt
, czyli kąt 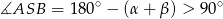
jest na pewno rozwarty. Zatem
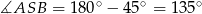 i korzystając z powyższej równości mamy
i korzystając z powyższej równości mamy 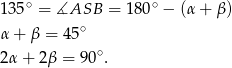
Zatem
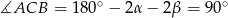 .
. Możemy więc wyliczyć długość odcinka
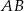 z twierdzenia Pitagorasa.
z twierdzenia Pitagorasa. 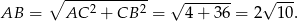
Odpowiedź: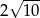
- Zauważmy, że ponieważ kąt
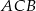 jest prosty to bok
jest prosty to bok 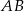 jest średnicą okręgu opisanego na trójkącie
jest średnicą okręgu opisanego na trójkącie 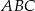 . W takim razie środek
. W takim razie środek 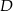 tego boku jest środkiem okręgu opisanego i
tego boku jest środkiem okręgu opisanego i 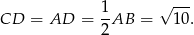
Odpowiedź: