/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 2327257

Dodaj do ulubionych
Dodaj do rozwiązanych

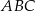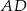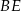W trójkącie ostrokątnym ABC wysokości AD i BE przecinają się w punkcie 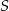S . Wiadomo, że 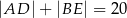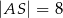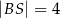|AD |+ |BE | = 20 , |AS | = 8 , |BS | = 4 . Wyznacz długości odcinków 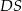DS i ES .

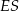Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

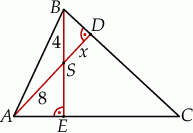
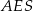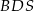Zauważmy, że trójkąty AES i BDS są oba prostokątne i mają wspólny kąt ostry

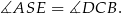
∡ASE = ∡DCB .

W takim razie są podobne i jeżeli oznaczymy 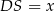DS = x , to

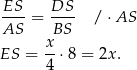
ES--= DS-- / ⋅AS AS BS x- ES = 4 ⋅8 = 2x .

Teraz pozostało skorzystać z podanego warunku 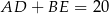AD + BE = 20 .

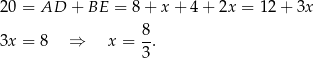
2 0 = AD + BE = 8+ x+ 4+ 2x = 12 + 3x 8 3x = 8 ⇒ x = -. 3

Stąd 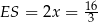ES = 2x = 16 3 .  
Odpowiedź: 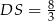8 DS = 3 , 16 ES = 3

Wersja PDF