Zadanie nr 2530955
Oto w jaki sposób można uzasadnić, że suma odległości dowolnego punktu 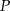 wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
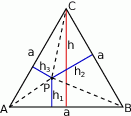
- Łączymy punkt
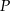 z wierzchołkami trójkąta i zapisujemy równość pól
z wierzchołkami trójkąta i zapisujemy równość pól 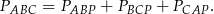
- Korzystamy ze wzoru na pole trójkąta
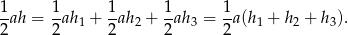
- Wnioskujemy, że
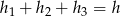 , a więc suma ta nie zależy od wyboru punktu
, a więc suma ta nie zależy od wyboru punktu  .
.
Postępując w analogiczny sposób wykaż, że suma odległości dowolnego punktu  wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu
wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu 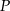 .
.
Rozwiązanie
Postępujemy analogicznie.
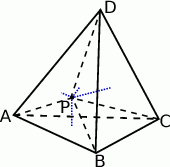
Łącząc punkt 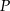 z wierzchołkami czworościanu, otrzymujemy 4 czworościany
z wierzchołkami czworościanu, otrzymujemy 4 czworościany 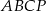 ,
, 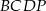 ,
, 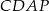 ,
, 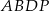 . Jeśli przez
. Jeśli przez 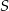 oznaczymy pole powierzchni każdej ze ścian czworościanu
oznaczymy pole powierzchni każdej ze ścian czworościanu 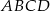 ,
, 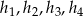 są odległościami punktu
są odległościami punktu 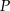 od ścian czworościanu, a
od ścian czworościanu, a 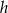 wysokością czworościanu to mamy równość objętości
wysokością czworościanu to mamy równość objętości
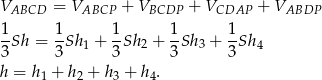
Tak jak w przypadku trójkąta, ponieważ suma ta jest równa wysokości czworościanu, nie zależy ona od wyboru punktu 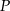 .
.

