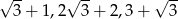/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 2574626

Dodaj do ulubionych
Dodaj do rozwiązanych

Jeden z kątów trójkąta prostokątnego ma miarę 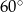∘ 60 , promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta.

Rozwiązanie

Zacznijmy od rysunku.

PIC

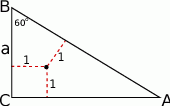
Jeżeli oznaczymy 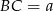BC = a , to z podanego kąta możemy wyliczyć długości pozostałych boków trójkąta

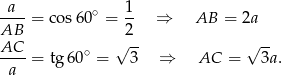
-a--= cos60∘ = 1- ⇒ AB = 2a AB 2 AC ∘ √ -- √ -- ----= tg 60 = 3 ⇒ AC = 3a. a

Skorzystamy teraz ze wozru na pole trójkąta 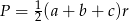P = 1(a + b + c)r 2 .

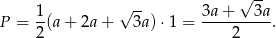
√ -- 1 √ -- 3a+ 3a P = -(a + 2a + 3a )⋅1 = ---------. 2 2

Z drugiej strony,

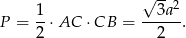
√ -- 1 3a2 P = --⋅AC ⋅CB = -----. 2 2

Zatem

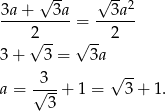
√ -- √ -- 3a + 3a 3a2 ----------= ------ 2√ -- √ -- 2 3+ 3 = 3a 3 √ -- a = √---+ 1 = 3+ 1. 3

 
Odpowiedź: √ -- √ -- √ -- 3 + 1,2 3 + 2 ,3 + 3

Wersja PDF