Zadanie nr 2672743
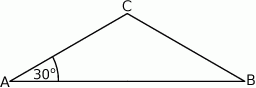
Kąt przy podstawie trójkąta równoramiennego 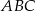 ma miarę
ma miarę 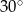 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta
. Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta 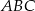 .
.
Rozwiązanie
Sposób I
Zauważmy, że jeżeli zbudujemy (narysujemy) trójkąt równoboczny 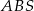 o boku równym podstawie danego trójkąta równoramiennego, to można go podzielić na 3 trójkąty przystające do trójkąta
o boku równym podstawie danego trójkąta równoramiennego, to można go podzielić na 3 trójkąty przystające do trójkąta 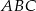 . W takim razie rzeczywiście
. W takim razie rzeczywiście
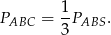
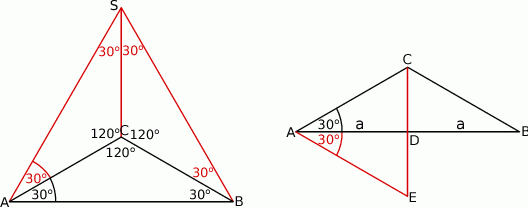
Sposób II
Oznaczmy długość podstawy trójkąta 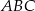 przez
przez 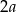 i niech
i niech 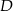 będzie środkiem podstawy
będzie środkiem podstawy 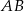 . Przy tych oznaczeniach pole trójkąta równobocznego o podstawie
. Przy tych oznaczeniach pole trójkąta równobocznego o podstawie 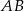 jest równe
jest równe
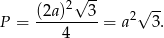
Zauważmy, że z trójkątów 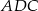 i
i 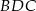 można zbudować trójkąt równoboczny
można zbudować trójkąt równoboczny 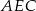 o wysokości
o wysokości 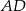 (prawy rysunek). Jeżeli przez
(prawy rysunek). Jeżeli przez  oznaczymy długość boku trójkąta
oznaczymy długość boku trójkąta 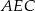 , to ze wzoru na wysokość trójkąta równobocznego mamy
, to ze wzoru na wysokość trójkąta równobocznego mamy
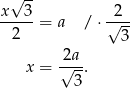
Korzystamy teraz ponownie ze wzoru na pole trójkąta równobocznego.