Zadanie nr 2692949
Z wierzchołka kąta prostego trójkąta prostokątnego 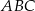 poprowadzono wysokość
poprowadzono wysokość 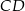 , która podzieliła przeciwprostokątną
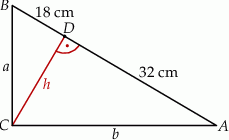
, która podzieliła przeciwprostokątną 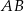 na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
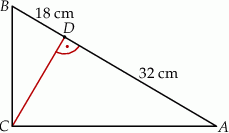
Oblicz pole trójkąta 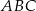 .
.
Rozwiązanie
Oznaczmy: 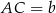 ,
, 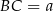 i
i 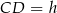 .
.
Sposób I
Na danym rysunku są 3 trójkąty prostokątne: 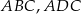 i
i 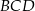 . Piszemy twierdzenie Pitagorasa w każdym z tych trójkątów.
. Piszemy twierdzenie Pitagorasa w każdym z tych trójkątów.
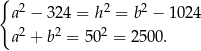
Z pierwszego równania mamy 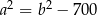 . Podstawiamy tę wartość do drugiego równania
. Podstawiamy tę wartość do drugiego równania
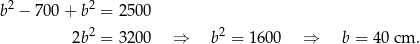
Stąd
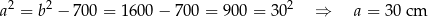
i pole trójkąta 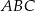 jest równe
jest równe
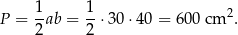
Sposób II
Trójkąty 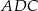 i
i 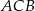 są prostokątne i mają wspólny kąt przy wierzchołku
są prostokątne i mają wspólny kąt przy wierzchołku 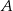 . Są więc podobne i mamy
. Są więc podobne i mamy
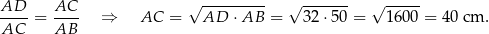
Analogicznie, z podobieństwa trójkątów 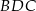 i
i 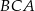 mamy
mamy
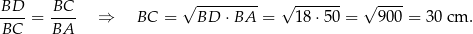
Pole trójkąta 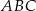 jest równe
jest równe
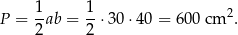
Odpowiedź: