Zadanie nr 2833564
W trójkącie równoramiennym 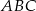 (
(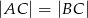 ) miara kąta
) miara kąta 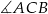 jest równa
jest równa 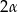 . Promień okręgu wpisanego w ten trójkąt ma długość
. Promień okręgu wpisanego w ten trójkąt ma długość  . Oblicz długości boków trójkąta
. Oblicz długości boków trójkąta 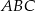 .
.
Rozwiązanie
Sposób I
Zacznijmy od rysunku i oznaczmy długość podstawy trójkąta przez 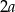 (
(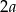 , a nie
, a nie  , żeby nie mieć ułamków).
, żeby nie mieć ułamków).
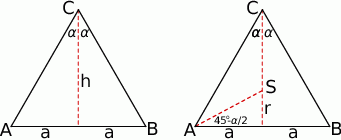
Aby wykorzystać podaną informację o promieniu okręgu wpisanego w trójkąt 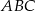 , będziemy chcieli skorzystać ze wzoru na pole
, będziemy chcieli skorzystać ze wzoru na pole 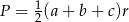 . Aby to zrobić musimy wyliczyć długości boków trójkąta (przy okazji wyliczymy też jego wysokość).
. Aby to zrobić musimy wyliczyć długości boków trójkąta (przy okazji wyliczymy też jego wysokość).
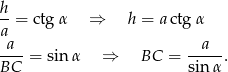
Zatem ze wspomnianego wzoru na pole trójkąta, mamy
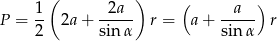
Z drugiej strony
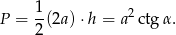
Mamy zatem
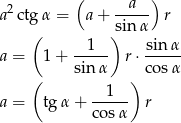
Zatem boki trójkąta wynoszą
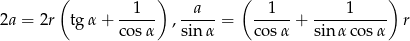
Sposób II
Podobnie jak w poprzednim sposobie zauważamy, że 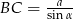 , ale tym razem w inny sposób wyliczymy
, ale tym razem w inny sposób wyliczymy  . Zauważmy, że kąt ostry przy podstawie trójkąta
. Zauważmy, że kąt ostry przy podstawie trójkąta 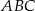 jest równy
jest równy 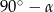 , zatem jeżeli połączymy wierzchołek
, zatem jeżeli połączymy wierzchołek 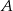 ze środkiem okręgu wpisanego (jest fragment dwusiecznej kąta
ze środkiem okręgu wpisanego (jest fragment dwusiecznej kąta 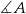 ) to otrzymamy trójkąt prostokątny z kątem ostrym
) to otrzymamy trójkąt prostokątny z kątem ostrym 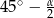 i przyprostokątnych długości
i przyprostokątnych długości  i
i  . Mamy więc
. Mamy więc
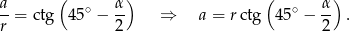
Odpowiedź: 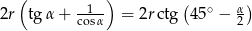 i
i