Zadanie nr 3106027

Oblicz długość boku kwadratu wpisanego w trójkąt równoboczny o boku .

Rozwiązanie

Zaczynamy od rysunku

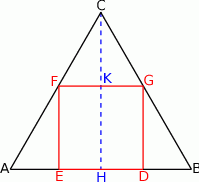
Oznaczmy przez długość boku kwadratu.

Sposób I

Ponieważ odcinek 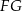jest równoległy do podstawy 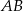, więc trójkąt 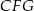CF G jest podobny do trójkąta 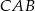CAB , czyli też jest równoboczny.

Odcinek 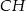jest wysokością trójkąta 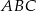ABC , więc

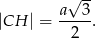
√ -- a--3- |CH | = 2 .

Zauważmy, że

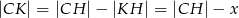
|CK | = |CH |− |KH | = |CH |− x

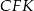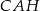Ponieważ trójkąty CF K i CAH są podobne mamy

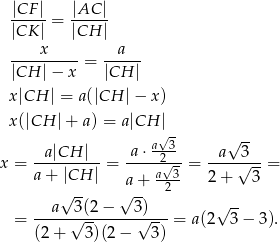
|CF | |AC | ----- = ------ |CK | |CH | ----x-----= --a--- |CH |− x |CH | x|CH | = a(|CH |− x ) x(|CH |+ a) = a|CH | a√ 3 √ -- --a|CH-|- -a⋅--2-- --a--3-- x = a + |CH | = a√-3= 2 + √ 3-= √ -- √a-+ 2 a 3(2 − 3) √ -- = -----√--------√---- = a(2 3 − 3). (2 + 3 )(2− 3)

Sposób II

Zauważmy, że

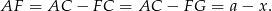
AF = AC − FC = AC − F G = a− x.

Patrzymy teraz na trójkąt prostokątny 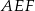AEF . Mamy w nim

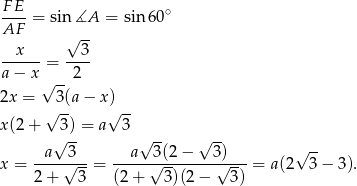
FE ----= sin ∡A = sin 60∘ AF √ -- --x--- --3- a− x = 2 √ -- 2x = √3(a − x)√ -- x(2+ 3) = a 3 √ -- √ -- √ -- --a--3-- --a--3-(2−----3)--- √ -- x = √ --= √ -- √ -- = a(2 3− 3). 2 + 3 (2 + 3)(2 − 3)

Odpowiedź: √ -- a(2 3 − 3)