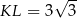Zadanie nr 3222851
Trójkąt równoboczny 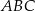 ma pole równe
ma pole równe 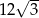 . Prosta równoległa do boku
. Prosta równoległa do boku 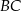 przecina boki
przecina boki 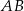 i
i 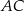 – odpowiednio – w punktach
– odpowiednio – w punktach 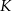 i
i 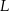 . Stosunek obwodów trójkątów
. Stosunek obwodów trójkątów 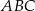 i
i 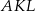 jest równy
jest równy 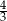 . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 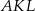 .
.
Rozwiązanie
Zaczynamy od rysunku
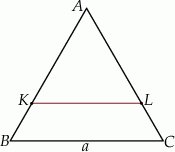
Jeżeli oznaczymy przez  długość boku trójkąta
długość boku trójkąta 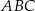 , to z podanego pola otrzymujemy
, to z podanego pola otrzymujemy
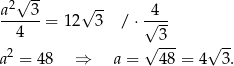
Wiemy ponadto, że trójkąty 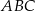 i
i 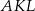 są podobne w skali
są podobne w skali
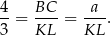
Stąd
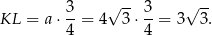
Odpowiedź: