/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 3224659

Dodaj do ulubionych
Dodaj do rozwiązanych

Promień okręgu opisanego na trójkącie prostokątnym ma długość 3 dm, a długość promienia okręgu wpisanego w trójkąt prostokątny wynosi 1 dm. Oblicz obwód tego trójkąta.

Rozwiązanie

Zaczynamy od rysunku.

PIC

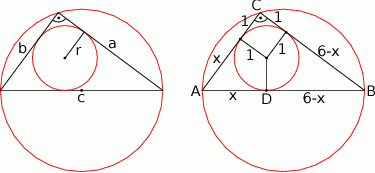
Średnicą okręgu opisanego na trójkącie prostokątnym jest przeciwprostokątna, więc

c = 2R = 6.

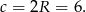
Sposób I

Korzystamy ze wzoru

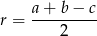
a+ b− c r = --------- 2

na promień okręgu wpisanego w trójkąt prostokątny. Mamy zatem

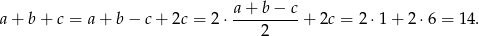
a + b− c a + b + c = a + b − c+ 2c = 2 ⋅---------+ 2c = 2 ⋅1+ 2⋅ 6 = 14. 2

Sposób II

Połączmy środek okręgu wpisanego w trójkąt z punktami styczności z bokami trójkąta oraz oznaczmy 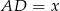AD = x . Wtedy 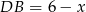DB = 6− x , z przyprostokątne mają długości

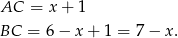
AC = x + 1 BC = 6 − x + 1 = 7 − x .

Obwód trójkąta jest więc równy

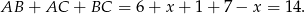
AB + AC + BC = 6+ x+ 1+ 7− x = 14.

 
Odpowiedź: 14 dm

Wersja PDF