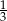/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 3347166

Dodaj do ulubionych
Dodaj do rozwiązanych

Miara jednego z kątów ostrych w trójkącie prostokątnym jest równa α .

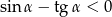  • Uzasadnij, że spełniona jest nierówność sin α− tg α < 0 .
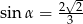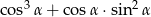  • Dla √ - sin α = 2--2 3 oblicz wartość wyrażenia cos3α + co sα ⋅sin 2α .

Rozwiązanie

Naszkicujmy sobie taki trójkąt

PIC

  •  

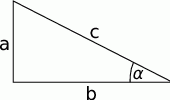
    Sposób I

    Przy oznaczeniach z obrazka, mamy

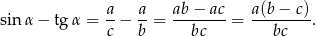
    a a ab− ac a(b − c) sinα − tg α = --− --= --------= -------- . c b bc bc

    Ponieważ przeciwprostokątna jest dłuższa od każdej z przyprostokątnych mamy 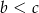b < c , co dowodzi żądanej nierówności.

    Sposób II

    Tym razem rozpiszmy tangens na sinus i cosinus.

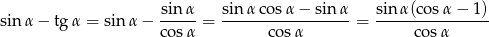
    sinα sin αco sα − sin α sin α(cos α− 1) sinα − tg α = sin α− ----- = ------------------ = ---------------- cos α cosα cosα

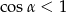    Teraz widać, że licznik jest ujemny, bo cos α < 1 .

  • Zauważmy, że
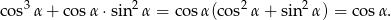
    cos3α + co sα ⋅sin2α = cosα (cos2α + sin2α ) = cosα .

    Wystarczy zatem obliczyć 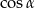cosα . Liczymy (z jedynki trygonometrycznej, α jest katem ostrym!).

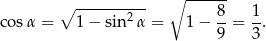
    ∘ ------ ∘ -------2-- 8- 1- co sα = 1− sin α = 1− 9 = 3.

     
    Odpowiedź: 13

Wersja PDF