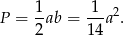/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 3521112

Dodaj do ulubionych
Dodaj do rozwiązanych

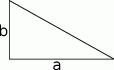
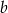Długości a i b przyprostokątnych trójkąta prostokątnego spełniają równość

a 2 − 6ab − 7b 2 = 0.
  • Oblicz tangensy kątów ostrych tego trójkąta.
  • Uzasadnij, że pole tego trójkąta jest równe -1a2 14 .

Rozwiązanie

  •  

    Sposób I

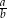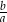    Ponieważ tangensy są równe a b i b a , podzielmy daną równość przez 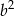b2 , żeby mieć właśnie takie wyrażenia (równie dobrze możemy podzielić przez 2 a ).

    PIC
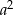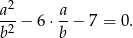
    a2- a- b2 − 6⋅ b − 7 = 0.

    Podstawmy teraz a t = b .

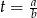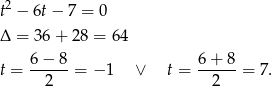
    2 t − 6t − 7 = 0 Δ = 36+ 28 = 64 t = 6-−-8-= − 1 ∨ t = 6-+-8-= 7 . 2 2

    Tangens kąta ostrego jest dodatni, więc 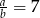a= 7 b . Stąd b= 1 a 7 .

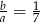    Sposób II

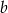    Zamiast dzielić podane wyrażenie przez a lub b mogliśmy rozłożyć je na czynniki.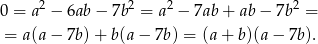

    2 2 2 2 0 = a − 6ab − 7b = a − 7ab + ab− 7b = = a(a − 7b) + b(a − 7b) = (a + b)(a − 7b ).

    Ponieważ 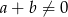a + b ⁄= 0 mamy stąd 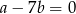a − 7b = 0 i dalej liczymy jak poprzednio.  
    Odpowiedź: 7 i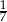 1 7

  • Z poprzedniego podpunktu wiemy, że 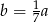1 b = 7a , zatem pole jest równe
    P = 1ab = -1a 2. 2 14
Wersja PDF