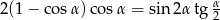/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 3676056

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równoramiennym kąt przy podstawie ma miarę α . Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na nim.

Rozwiązanie

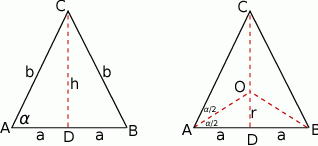
Przyjmijmy oznaczenia z rysunku, tzn. niech 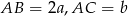AB = 2a,AC = b .

PIC

Sposób I

Promień okręgu opisanego możemy łatwo wyliczyć z twierdzenia sinusów.

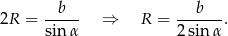
2R = -b--- ⇒ R = --b---. sin α 2sinα

Promień okręgu wpisanego wyliczymy ze wzoru na pole

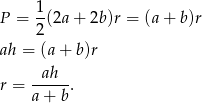
1 P = -(2a + 2b )r = (a+ b)r 2 ah = (a+ b)r ah r = -----. a+ b

Ponadto

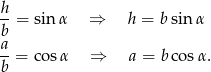
h --= sin α ⇒ h = b sinα ba --= cos α ⇒ a = bcos α. b

Zatem szukany iloraz

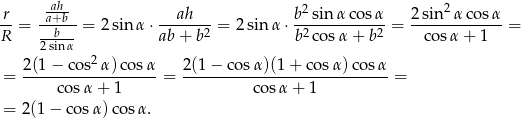
-r -aah+b-- ---ah--- b2sinα-cos-α- 2sin2α-cos-α- R = --b-- = 2 sin α ⋅ab + b2 = 2sin α⋅ b2cos α+ b2 = co sα + 1 = 2sin α 2(1− cos2α )cos α 2 (1− co sα)(1 + co sα)c osα = -------------------= ---------------------------- = co sα + 1 cos α+ 1 = 2 (1− co sα) cosα .

Sposób II

Tym razem promień okręgu wpisanego obliczmy z trójkąta 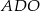ADO , gdzie 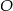O jest środkiem okręgu wpisanego.

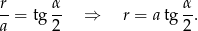
r-= tg α- ⇒ r = a tg α. a 2 2

Żeby we wzorze na promień okręgu opisanego mieć a wykorzystamy twierdzenie sinusów dla kąta 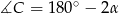∡C = 180∘ − 2α .

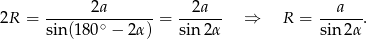
2R = ------2a------- = --2a-- ⇒ R = ---a--. sin(180∘ − 2α ) sin 2α sin 2α

Szukany iloraz

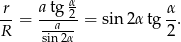
r atg α α --= --a-2-= sin 2α tg--. R sin2α 2

 
Odpowiedź: 2(1 − cos α)co sα = sin 2α tg α 2

Wersja PDF