/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 3774654

Dodaj do ulubionych
Dodaj do rozwiązanych

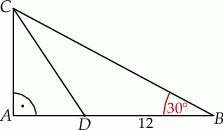
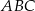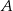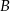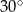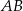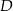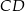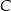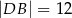W trójkącie ABC kąt przy wierzchołku A jest prosty, a kąt przy wierzchołku B ma miarę 30∘ . Na boku AB tego trójkąta obrano punkt D tak, że odcinek CD jest dwusieczną kąta przy wierzchołku C oraz |DB | = 12 (zobacz rysunek). Oblicz |AD | .

PIC

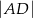Rozwiązanie

Zauważmy, że

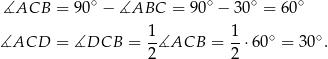
∡ACB = 90∘ − ∡ABC = 90∘ − 30∘ = 60∘ 1- 1- ∘ ∘ ∡ACD = ∡DCB = 2∡ACB = 2 ⋅60 = 30 .

To oznacza, że trójkąt 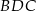BDC jest równoramienny, czyli 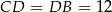CD = DB = 12 oraz

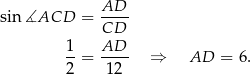
AD-- sin ∡ACD = CD 1 AD --= ---- ⇒ AD = 6. 2 12

 
Odpowiedź: 6

Wersja PDF